
本記事では、NUS MSBA在籍のTakaさんが興味深いと感じた授業の1つである「ANALYTICS IN MANAGERIAL ECONOMICS」について、より具体的な授業内容をご紹介します。
ANALYTICS IN MANAGERIAL ECONOMICSとは!?
大学の経済学部やMBAで学ぶようなミクロ経済学の基礎を扱いました。更に計量経済学で使われるデータ分析手法についてもグループプロジェクトを通して学びました。
印象的だったのは、教授は事あるごとに以下のメッセージを学生へ訴えていたことです。
今はツールを使えばだれでも機械学習ができる時代だ。私の妻や娘でさえ、機械学習が出来てしまうんだ。だが、分析対象データの内生性や因果性を考慮した適切な分析を行わないと、仮にどんな複雑なモデルを作ったとしても、誤った結果や偏った結果を容易に導き出してしまう。だから、この授業で扱う計量経済学の手法を理解する必要があるんだ。
データサイエンティストの仕事というと、機械学習やAI(人工知能)などの最先端技術を使うことに注目が集まっていますが、この授業では安易な考えで複雑なモデルを作ってビジネス課題を解決しようとする事への警鐘を鳴らしていた事が印象的でした。
この授業では特にグループプロジェクトを通しての学びが大きかったので、当記事ではグループプロジェクトについてご紹介します。グループプロジェクトでは4~5人のチームを作ってディスカッションしながらデータ分析を行い、レポートを提出しました。
<計量経済学とは>
計量経済学とは、統計学や経済学の理論および手法を用いて、仮説や政策効果の検証・将来予測を行う学問です。
グループプロジェクト1:コーヒーの需要曲線と供給曲線の推定
このプロジェクトでは、過去の統計データを用いてオランダでのコーヒーの需要曲線と供給曲線の推定を行いました。
需要曲線の場合は、需要と価格の関係がln(Q)=α×ln(P)+µのモデルで表現できると仮定し、過去の統計データを用いて未知の係数αの値を推定します。αの値を推定することで価格弾力性を知ることができ、コーヒーを販売する際の価格付けの戦略に活かすことができます。
推定手法として回帰分析を使いますが、このケースでは通常の回帰分析を使ってもバイアスがかかった結果しか得られません。なぜならば、内生性バイアスという問題が生じるからです。通常の回帰分析を使ってαを推定すると内生性バイアスと呼ばれる偏りがかかった結果が出てしまい、正しく需要曲線の形を推定することが出来ません。
そこで、操作変数法と呼ばれる手法を使って、内生性バイアスを排除した上での需要曲線の推定を行いました。この手法を用いる上では適切な操作変数を選択することが重要になりますが、操作変数の選ぶ際には、純粋な数学の知識よりも事象の背景の理解(=ビジネスセンス)が要求されます。
<用語解説>
ln(Q):コーヒー需要量の自然対数をとったもの
ln(P):コーヒー価格の自然対数をとったもの
µ:誤差項と呼ばれ、「需要量に影響を与えるが、定量化することが困難な要因」による影響
内生性バイアス:P(コーヒー価格)とµ(誤差)の間に相関があるために生じるバイアス
グループプロジェクト2:金融政策が銀行のトレーディング戦略に及ぼした影響の評価
このプロジェクトでは、「差分の差分法」を使った因果推論を行いました。なんと、教授が2016年6月に発表したばかりの最新の論文のシナリオに沿う形で分析を進めていきました。
具体的には、2008年の金融危機後に銀行に課された規制の1つであるボルカー・ルールが銀行のトレーディングビジネスに与えた影響の評価を行いました。このルールにより銀行はリスクが高い市場取引を制限されることになります。
<ボルカー・ルールとは>
ボルカー・ルールは、2008年の金融危機後にアメリカで成立したドット・フランク法の中の1つで、銀行の自己勘定取引(自己資金を元手に利益を狙う取引)を規制することを目的としています。
直感的には「ボルカー・ルールが発表された前後での、銀行の自己勘定取引の割合の変化」を調べることで政策の効果を測れるように思われますが、実際にはこれでは効果を正しく評価することはできません。何故ならば、ボルカー・ルールの発表以外にも、銀行の自己勘定取引へ影響を与えた要因が存在する可能性があるからです。そこで、このボルカー・ルールと自己勘定取引の変化の因果関係を分析するために差分の差分法という手法を用いました。
当プロジェクトでは、対象の銀行を2つのグループ(処置群と対照群)に分けて分析を行いました。(図1参照)
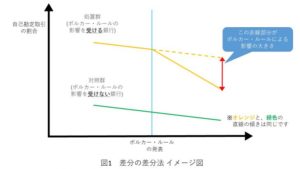
処置群にはボルカー・ルールの影響を強く受けると考えられる銀行(ルール発表前の自己勘定取引比率が高かった銀行)が入り、対照群はボルカー・ルールの影響を受けないと考えられる銀行(ルール発表前の自己勘定取引比率が低かった銀行)が入ることになります。
これら2つのグループ各々について、ボルカー・ルール発表前後での自己勘定取引の割合変化を計算することで、他の要因(景気変動など)による影響を排除した上で政策の効果を測定することができます。
「同時期にボルカールールの影響を受ける状況にあったか」の観点のみで各銀行をグループ分けしているので、ボルカー・ルール以外に自己勘定取引へ影響を与えるファクターを排除した比較をすることができることになります。中学校の理科で勉強した「対照実験」と同じ考え方ですね。
この「差分の差分法」は、このような政策の評価だけではなくビジネスでも活用されています。例えば広告を打ったことによる効果がどれぐらいあったのかを評価する、といった物事の因果関係の分析用途で使われています。
